Главные формулы для егэ по профильной математике

Какие темы важно знать для ЕГЭ по математике 2022?

В математике, как и в любом предмете, есть опорные темы. Если вы их выучите, будет легче справиться с экзаменом.

Формулы тригонометрии

Очень важно знать формулы тригонометрии и уметь применять их. Хорошая новость: в справочных материалах можно найти несколько тригонометрических формул

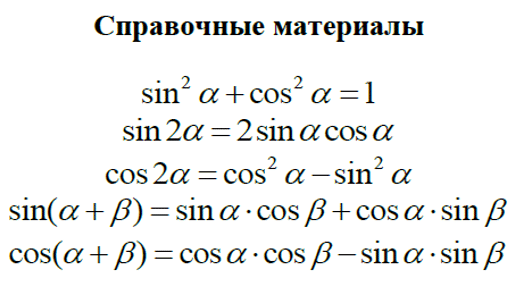
Но формул гораздо больше. Я советую не зубрить их, а научиться выводить: приходить к формулам шаг за шагом, опираясь на тождества. Кстати, мы учим выводить формулы на курсах подготовки к ЕГЭ: это полезно, чтобы оказаться на экзамене во всеоружии и ничего не перепутать.

Квадратные уравнения

Эти уравнения мы учимся решать еще в 7 классе. Они встречаются в ЕГЭ по математике постоянно: и как самостоятельные задания, и внутри более сложных уравнений или неравенств. Квадратные уравнения могут встретиться в математических моделях № 8 и № 15, в задачах на геометрию и стереометрию, в задании № 17 с параметром.

Самое главное — хорошо знать универсальные методы решения. Первый — через формулу дискриминанта, второй — через теорему Виета, которая может сэкономить время на экзамене.

Треугольники

Эта замечательная тема, которую проходят в 7 классе — основа основ всей геометрии. Она нужна и для решения стереометрии. и для простейших планиметрических задач. Еще треугольники необходимы, чтобы освоить огромное количество теорем

Выучите все, что с ними связано! Особое внимание обратите на прямоугольные треугольники, которые встречаются чаще остальных — тогда геометрические задачи сразу станут проще

Проценты

Самая нелюбимая тема моих учеников после тригонометрии, которую необходимо хорошо знать. Проценты нужны для реальной математики — это № 8 (с кратким ответом) и № 15 (с развернутым ответом). Понимание этой темы может принести вам 3 первичных балла.

Дробно рациональные уравнения

• Если дробь равна нулю, то числитель равен нулю, а знаменатель не равен нулю.
• Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно-рациональным.

Чтобы решить дробно рациональное уравнение, необходимо:

1. Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ)
2. Найти общий знаменатель дробей, входящих в уравнение;
3. Умножить обе части уравнения на общий знаменатель;
4. Решить получившееся целое уравнение;
5. Исключить из его корней те, которые не удовлетворяют условию ОДЗ.

Если в уравнении участвуют две дроби и числители их равные выражения, то знаменатели можно приравнять друг к другу и решить полученное уравнение, не обращая внимание на числители. НО учитывая ОДЗ всего первоначального уравнения

Задача №17, экономическая

Стандартное начало условия:

• 1-го числа каждого месяца долг возрастает на `color(green)(r%)`.
• со 2-го по 14-е число каждого месяца необходимо выплатить часть долга.
• 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Основная идея решения:

1. каждый месяц (15-го числа) долг должен уменьшаться на одну и ту же величину, т.е. на `1/n` часть изначального долга, т.е. на `color(blue)(S/n)`
2. каждый месяц (1-го числа) банк увеличивает остаток долга на `color(green)(r%)`.
3. каждый месяц (2-14-го числа) клиент выплачивает начисленные проценты (пункт 2) и ежемесячную часть долга (пункт 1).

Составляем таблицу платежей по месяцам:

Взятие кредита:
15 декабря:	Долг = `S` рублей.
1-й месяц:
1 января	Банк начисляет проценты = `color(green)(S*r)`
	Долг = `S + color(green)(S*r)`
2-14 января	Платим `color(green)(S*r) + color(blue)(S/n)`
	Долг = « `– [ color(green)(S*r) + color(blue)(S/n) ] = S-color(blue)(S/n) = (n-1)/n*S`
2-й месяц:
1 февраля	Банк начисляет проценты = `color(green)(obrace((n-1)/n*S)^(«Предыд.долг»)*r)`
	Долг = `(n-1)/n*S+` `color(green)((n-1)/n*S*r)`
2-14 февраля	Платим `color(green)((n-1)/n*S*r)+` `color(blue)(S/n)`
	Долг = `[(n-1)/n*S +` `color(green)((n-1)/n*S*r)]–` `[color(green)((n-1)/n*S*r)+` `color(blue)(S/n)]=` `(n-1)/n*S — color(blue)(S/n)=` `(n-2)/n*S`
3-й месяц:
1 марта	Банк начисляет проценты = `color(green)((n-2)/n*S*r)`
	Долг = `(n-2)/n*S + color(green)((n-2)/n*S*r)`
2-14 марта	Платим `color(green)((n-2)/n*S*r) + color(blue)(S/n)`
	Долг = `[(n-2)/n*S + color(green)((n-2)/n*S*r)] – [color(green)((n-2)/n*S*r) + color(blue)(S/n)] = (n-2)/n*S — color(blue)(S/n) = (n-3)/n*S`
(n-1)-й месяц:	Остаток долга = `2/n*S`
1 мартобря	Банк начисляет проценты = `color(green)(2/n*S*r)`
	Долг = `2/n*S + color(green)(2/n*S*r)`
2-14 мартобря	Платим `color(green)(2/n*S*r) + color(blue)(S/n)`
	Долг = `[2/n*S + color(green)(2/n*S*r)] – [color(green)(2/n*S*r) + color(blue)(S/n)] = 2/n*S — color(blue)(S/n) = 1/n*S`
n-й месяц:	Остаток долга = `1/n*S`
1 апребря	Банк начисляет проценты = `color(green)(1/n*S*r)`
	Долг = `1/n*S + color(green)(1/n*S*r)`
2-14 апребря	Платим `color(green)(1/n*S*r) + color(blue)(S/n)`
	Долг = `[1/n*S + color(green)(1/n*S*r)] – [color(green)(1/n*S*r) + color(blue)(S/n)] = 1/n*S — color(blue)(S/n) = 0`

Формулы по базовой математике для ЕГЭ

Разработчики КИМ считают, что для решения задач математики ЕГЭ базового уровня достаточно знания формул, представленных в справочных материалах – они выдаются на экзамене в индивидуальном комплекте вместе с КИМ. В «официальную шпаргалку», которой можно пользоваться во время проведения ЕГЭ, входят:

• таблица квадратных чисел от 0 до 99;
• свойства арифметического квадратного корня;
• формулы сокращенного умножения;
• корни квадратного уравнения;
• свойства степени и логарифма;
• теорема Пифагора;
• формула расчета длины окружности и площади круга;
• расчет средней линии треугольника и трапеции;
• радиус вписанной и описанной окружности правильного треугольника;
• формулы расчета площади планиметрических фигур;
• вычисление поверхностей и объемов тел;
• основные тригонометрические функции и тождества;
• график линейной функции;
• геометрический смысл производной.

Понять, нужны ли еще какие-то формулы для ЕГЭ по математике, поможет решение тренировочных тестов, например, содержащихся в открытом банке заданий на сайте ФИПИ. Для подстраховки можно изучить КЭС (кодификатор элементов содержания), актуальный в текущем учебном году. В нем перечислены все темы, которые выносятся на экзамен.

Решение 3-х более сложных уравнений

Уравнение 12. Най­ди­те корни урав­не­ния: \( \displaystyle cos\frac{8\pi x}{6}=\frac{\sqrt{3}}{2}\). В от­ве­те за­пи­ши­те наи­боль­ший от­ри­ца­тель­ный ко­рень.

Логика простая: будем поступать так, как поступали раньше не взирая на то, что теперь у тригонометрических функций стал более сложный аргумент!

Если бы мы решали уравнение вида:

\( \displaystyle cost=\frac{\sqrt{3}}{2}\)То мы бы записали вот такой ответ:

\( \displaystyle t=\pm arccos\frac{\sqrt{3}}{2}+2\pi n,~n\in Z\)Или (так как \( \displaystyle arccos\frac{\sqrt{3}}{2}=\frac{\pi }{6}\))

\( \displaystyle t=\pm \frac{\pi }{6}+2\pi n,~n\in Z\)Но теперь в роли \( \displaystyle t\) у нас выступаем вот такое выражение: \( \displaystyle t=\frac{8\pi x}{6}\)

Тогда можно записать:

\( \displaystyle \frac{8\pi x}{6}=\pm \frac{\pi }{6}+2\pi n\)Наша с тобою цель – сделать так, чтобы слева стоял просто \( \displaystyle x\), без всяких «примесей»!

Давай постепенно от них избавляться!

Вначале уберём знаменатель при \( \displaystyle x\): для этого домножим наше равенство на \( \displaystyle 6\):

\( \displaystyle \frac{6\cdot 8\pi x}{6}=6\cdot \left( \pm \frac{\pi }{6}+2\pi n \right)\)\( \displaystyle 8\pi x=\pm \frac{6\pi }{6}+12\pi n\)\( \displaystyle 8\pi x=\pm \pi +12\pi n\)Теперь избавимся от \( \displaystyle \pi \), разделив на него обе части:

\( \displaystyle 8x=\pm 1+12n\)Теперь избавимся от восьмёрки:\( \displaystyle \frac{8x}{8}=\pm \frac{1}{8}+\frac{12n}{8}\)\( \displaystyle x=\pm \frac{1}{8}+\frac{3n}{2}\)Полученное выражение можно расписать как 2 серии решений (по аналогии с квадратным уравнением, где мы либо прибавляем, либо вычитаем дискриминант)\( \displaystyle x=\frac{1}{8}+\frac{3n}{2}\)или\( \displaystyle x=-\frac{1}{8}+\frac{3n}{2}\)Нам нужно найти наибольший отрицательный корень! Ясно, что надо перебирать \( \displaystyle n\).

Квадратное уравнение и формула разложения квадратного трехчлена на множители

Пусть квадратное уравнение имеет вид:

Тогда дискриминант находят по формуле:

Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:

Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:

Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения может быть вычислено по формуле:

Парабола

График параболы задается квадратичной функцией:

При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:

Игрек вершины параболы:

Краткие конспекты по физике. 10-11 класс — в помощь застрявшим в пути

Подробности

Просмотров: 1006

Кинематика

Прямолинейное равномерное движение и решение задач ……… смотреть
Закон сложения скоростей и решение задач ……… смотреть
Движение с постоянным ускорением и решение задач ……… смотреть
Свободное падение ……… смотреть
Движение тела, брошенного под углом к горизонту ……… смотреть
Решение задач. Тело, брошенное под углом к горизонту ……… смотреть
Криволинейное движение ……… смотреть

Молекулярная физика. Термодинамика

Основные положения МКТ. Масса и размер молекул. Количество вещества ……… смотреть
Взаимодействие молекул. Строение твердых тел, жидкостей и газов ……… смотреть
Идеальный газ. Основное уравнение МКТ ……… смотреть
Температура. Тепловое равновесие. Абсолютная шкала температур ……… смотреть
Уравнение состояния идеального газа ……… смотреть
Изопроцессы. Газовые законы ……… смотреть
Взаимные превращения жидкостей и газов. Влажность воздуха ……… смотреть
Твердые тела. Кристаллические тела. Аморфные тела ……… смотреть

Электростатика

Электрический заряд. Электризация. Закон сохранения электрического заряда. Закон Кулона. Единица электрического заряда……… смотреть
Близкодействие и дальнодействие. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции полей. Силовые линии электрического поля……… смотреть
Проводники и диэлектрики в электростатическом поле. Поляризация диэлектриков……… смотреть
Потенциальная энергия тела в электростатическом поле. Потенциал электростатического поля и разность потенциалов. Связь между напряженностью электростатического поля и разхностью потенциалов……… смотреть
Электроемкость. Конденсаторы. Энергия заряженного конденсатора……… смотреть

Законы постоянного тока

смотретьсмотреть

Электрический ток в различных средах

Электронная проводимость металлов. Зависимость сопротивления проводника от температуры. Сверхпроводимость……… смотреть
Электрический ток в полупроводниках. Р-n переход. Полупроводниковые приборы……… смотреть
Электрический ток в вакууме. Вакуумный диод. Электронно-лучевая трубка……… смотреть
Электрический ток в жидкостях. Закон электролиза……… смотреть
Электрический ток в газах……… смотреть
Контрольные вопросы к зачету по теме: Электрический ток в различных средах………. смотреть

Электромагнитное поле

Взаимодействие токов. Магнитное поле. Вектор магнитной индукции. Сила Ампера ……… смотреть
Действие магнитного поля на движущийся заряд.Магнитные свойства вещества ……… смотреть
Явление электромагнитной индукции. Магнитный поток. Направление индукционного тока. Правило Ленца……… смотреть
ЭДС электромагнитной индукции. Вихревое электрическое поле……… смотреть
ЭДС индукции в движущихся проводниках……… смотреть
Самоиндукция. Индуктивность. Энергия магнитного поля. Вопросы к пр/работе ……… смотреть

Оптика

Природа света. Измерение скорости света ……… смотреть
Световой луч. Основные свойства линзы ……… смотреть
Построение изображения точки в линзах ……… смотреть
Построение изображения предмета в линзах ……… смотреть
Отражение света……… смотреть
Преломление света……… смотреть
Полное внутреннее отражение……… смотреть
Дисперсия света……… смотреть
Интерференция света……… смотреть
Дифракция света……… смотреть
Поляризация света……… смотреть

Атомная физика

Строение атома………
Квантовые постулаты Бора………
Методы регистрации и наблюдения элементарных частиц………
Естественная радиоактивность………
Виды радиоактивного распада………
Закон радиоактаивного распада………
Ядерные силы………
Открытие электрона, протона, нейтрона………
Строение ядра атома………
Изотопы………
Энергия связи ядра и дефект масс………
Ядерные реакции, энергетический выход ядерной реакции………
Деление ядер урана. Цепная реакция………
Ядерный реактор. Атомная бомба………
Термоядерная реакция. Водородная бомба………
Топливно-энергетические ресурсы. Ядерная энергетика………

Назад в раздел «10-11 класс»

Правила дифференцирования

1. Производная суммы или разности
2. Производная произведения
2a. Производная выражения, умноженного на постоянный множитель
3. Производная частного
4. Производная сложной функции

Правило 1. Если функции

дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции

причём

т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.

Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны, т.е.

Правило 2. Если функции

и

дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение

причём

т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой. 

Следствие 1. Постоянный множитель можно выносить за знак производной:

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.

Например, для трёх множителей:

Правило 3. Если функции

и

дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём

т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.

Где что искать на других страницах

При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций».

Здесь же (далее) — более простые примеры на производную произведения и частного, на которых Вы увереннее освоите алгоритмы вычислений.

Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме
и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она
выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных,
но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.

А если при дифференцировании произведения или частного у вас появилось слагаемое
, в котором — число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).

Другая частая ошибка — механическое решение производной сложной
функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.

По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.

Если Вы ищете решения производных дробей со степенями и корнями,
то есть, когда функция имеет вид вроде , то
следуйте на занятие «Производная суммы дробей со степенями и корнями».

Если же перед Вами задача вроде ,
то Вам на занятие «Производные простых тригонометрических функций».

Особенности уровней ЕГЭ по математике

В 2015 году ЕГЭ по математике разделили на базовый и профильный уровни. Это упростило жизнь выпускникам, которые не планируют поступать на специальности, связанные с математикой. Если ЕГЭ по математике нужен только для получения аттестата, можно сдать его облегченную версию, оставив время и силы для профильных экзаменов.

Базовый уровень ЕГЭ по математике

Как устроен базовый ЕГЭ по математике? Экзамен идет 180 минут, он состоит из 21 задания, за каждое из которых можно получить 1 балл. Этот экзамен единственный, который переводится не в 100-бальную систему, а в оценки.

Пока перевод баллов ЕГЭ по математике базового уровня в оценки не опубликован ФИПИ, но мы добавим его в статью, как только появится официальная информация.

В ЕГЭ по математике базового уровня 6 тематических блоков:

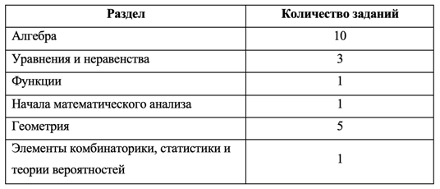
Тематические блоки, ЕГЭ по математике 2022, базовый уровень

Подробнее про базовый ЕГЭ по математике, включая разбор всех заданий, читайте здесь, а мы перейдём к профильному.

Профильный уровень ЕГЭ по математике

Данный экзамен, как и остальные ЕГЭ, переводится в 100-бальную систему.

Пока перевод баллов ЕГЭ по математике профильного уровня в 100-бальную систему пока не опубликован ФИПИ. Мы добавим его в статью, как только появится официальная информация.

Экзамен состоит из двух частей: Часть 1 с кратким ответом, а Часть 2 — с развернутым. Длится он 235 минут. Всего есть 18 заданий, которые разделены на 3 блока: алгебра, геометрия и реальная математика. Максимальное количество первичных баллов — 31.

База, профиль — неважно, к какому именно уровню вы готовитесь. В любом случае надо не только правильно решить каждое задание, но и оформить его так, чтобы проверяющие ни к чему не придрались

Нарисовать и описать график, расписать решение уравнения или задачи… И это не все: нужно еще и внести ответы в бланк без ошибок. И все это — за ограниченный период времени! Так можно перенервничать и запороть даже самую простую задачку. А на ЕГЭ — каждый балл на счету.Поэтому на своих занятиях я сразу показываю своим ученикам, как правильно оформлять каждое задание в ЕГЭ по математике. Мы разбираем все критерии и учимся правильно отвечать на вопросы. А еще я всегда помогаю ученикам закрыть пробелы в знаниях и объясняю сложные темы столько раз, сколько нужно. И куда же без лайфхаков? Всегда рассказываю лучший способ решения типичных заданий. Так что мои ученики приходят на экзамены подготовленными и не нервничают, когда видят задачу. Хотите также? Приходите ко мне на курсы подготовки к ЕГЭ по математике — научу!

Теория к заданию 7 из ЕГЭ по математике (профильной)

Производной функции $y = f(x)$ в данной точке $х_0$ называют предел отношения приращения функции к соответствующему приращению его аргумента при условии, что последнее стремится к нулю:

$f'(x_0)={lim}{△x→0}{△f(x_0)}/{△x}$

Дифференцированием называют операцию нахождения производной.

Таблица производных некоторых элементарных функций

Функция	Производная
$c$	$0$
$x$	$1$
$x^n$	$nx^{n-1}$
${1}/{x}$	$-{1}/{x^2}$
$√x$	${1}/{2√x}$
$e^x$	$e^x$
$lnx$	${1}/{x}$
$sinx$	$cosx$
$cosx$	$-sinx$
$tgx$	${1}/{cos^2x}$
$ctgx$	$-{1}/{sin^2x}$

Основные правила дифференцирования

1. Производная суммы (разности) равна сумме (разности) производных

$(f(x) ± g(x))’= f'(x)±g'(x)$

Найти производную функции $f(x)=3x^5-cosx+{1}/{x}$

Производная суммы (разности) равна сумме (разности) производных.

$f'(x) = (3x^5 )’-(cos x)’ + ({1}/{x})’ = 15x^4 + sinx — {1}/{x^2}$

2. Производная произведения

$(f(x) · g(x))’= f'(x) · g(x)+ f(x) · g(x)’$

Найти производную $f(x)=4x·cosx$

$f'(x)=(4x)’·cosx+4x·(cosx)’=4·cosx-4x·sinx$

3. Производная частного

$({f(x)}/{g(x)})’={f'(x)·g(x)-f(x)·g(x)’}/{g^2(x)}$

Найти производную $f(x)={5x^5}/{e^x}$

$f'(x)={(5x^5)’·e^x-5x^5·(e^x)’}/{(e^x)^2}={25x^4·e^x-5x^5·e^x}/{(e^x)^2}$

4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции

$f(g(x))’=f'(g(x))·g'(x)$

$f(x)= cos(5x)$

$f'(x)=cos'(5x)·(5x)’=-sin(5x)·5= -5sin(5x)$

Физический смысл производной

Если материальная точка движется прямолинейно и ее координата изменяется в зависимости от времени по закону $x(t)$, то мгновенная скорость данной точки равна производной функции.

$v(t) = x'(t)$

Точка движется по координатной прямой согласно закону $x(t)= 1,5t^2-3t + 7$, где $x(t)$ — координата в момент времени $t$. В какой момент времени скорость точки будет равна $12$?

Решение:

1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции

$v(t) = x'(t) = 1,5·2t -3 = 3t -3$

2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:

$3t-3 = 12$

$3t = 15$

$t = 5$

Ответ: $5$

Геометрический смысл производной

Напомним, что уравнение прямой, не параллельной осям координат, можно записать в виде $y = kx + b$, где $k$ – угловой коэффициент прямой. Коэффициент $k$ равен тангенсу угла наклона между прямой и положительным направлением оси $Ох$.

$k = tgα$

Производная функции $f(x)$ в точке $х_0$ равна угловому коэффициенту $k$ касательной к графику в данной точке:

$f'(x_0) = k$

Следовательно, можем составить общее равенство:

$f'(x_0) = k = tgα$

На рисунке касательная к функции $f(x)$ возрастает, следовательно, коэффициент $k > 0$. Так как $k > 0$, то $f'(x_0) = tgα > 0$. Угол $α$ между касательной и положительным направлением $Ох$ острый.

На рисунке касательная к функции $f(x)$ убывает, следовательно, коэффициент $k < 0$, следовательно, $f'(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.

На рисунке касательная к функции $f(x)$ параллельна оси $Ох$, следовательно, коэффициент $k = 0$, следовательно, $f'(x_0) = tg α = 0$. Точка $x_0$, в которой $f ‘(x_0) = 0$, называется экстремумом.

На рисунке изображён график функции $y=f(x)$ и касательная к этому графику, проведённая в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.

Решение:

Касательная к графику возрастает, следовательно, $f'(x_0) = tg α > 0$

Для того, чтобы найти $f'(x_0)$, найдем тангенс угла наклона между касательной и положительным направлением оси $Ох$. Для этого достроим касательную до треугольника $АВС$.

Найдем тангенс угла $ВАС$. (Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету.)

$tg BAC = {BC}/{AC} = {3}/{12}= {1}/{4}=0,25$

$f'(x_0) = tg ВАС = 0,25$

Ответ: $0,25$

Производная так же применяется для нахождения промежутков возрастания и убывания функции:

Если $f'(x) > 0$ на промежутке, то функция $f(x)$ возрастает на этом промежутке.

Если $f'(x) < 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.

На рисунке изображен график функции $y = f(x)$. Найдите среди точек $х_1,х_2,х_3…х_7$ те точки, в которых производная функции отрицательна.

В ответ запишите количество данных точек.

Решение:

Отрицательным значениям производной соответствуют интервалы, на которых функция $f (x)$ убывает. Поэтому, выделим на рисунке интервалы, на которых функция убывает.

В выделенных интервалах находятся точки $х_2, х_4$. В ответ напишем их количество $2$.

Ответ: $2$

Можешь дать какой-то совет тем, кто планирует сдавать ЕГЭ по профильной математике?

Не бойтесь математики. Многие говорят, что это сложный и страшный экзамен: варианты в книжках и на сайтах сложнее самого экзамена, поэтому учителя и репетиторы просто запугивают этими вариантами. На самом деле, если готовиться к экзамену и решать задания именно с реальных ЕГЭ, можно написать его на очень высокий балл.

Важно при этом не зазубривать формулы и не заучивать алгоритмы решений, а именно понимать, что происходит в задаче и как её можно решить. Если у вас слабая база, то начинать готовиться нужно в 10-м классе, а с хорошей базой можно, наверно, и в 11-м начать, но в начале года, а не весной

Если у вас слабая база, то начинать готовиться нужно в 10-м классе, а с хорошей базой можно, наверно, и в 11-м начать, но в начале года, а не весной.

Изображение на обложке: Monograph / Dribbble

Задания второй части профильного экзамена

В эту часть вошли непростые, комбинированные задачи, однако научиться решать можно каждую.

Задание №13 посвящено уравнениям: тригонометрическим, показательным и другим. Всё чаще в этом номере дают комбинаторное уравнение — логарифм плюс тригонометрия и другие вариации.

В задании №14 вам предлагается решить стереометрическую задачу. Она может быть на объём многогранников и их сечения или нахождение расстояния между прямой и плоскостью. Чтобы решить эти задачи, нужно хорошо знать теорию и много практиковаться. 

В задании №15 вам встретятся неравенства: смешанные, иррациональные или неравенства, содержащие модуль.

Для решения задачи №16 нужны твёрдые знания по планиметрии. Это задание проверяет ваше умение находить элементы трапеции, треугольника, окружности и других фигур. 

Задание №17 часто называют экономикой, так как оно связано с финансовой математикой. Вам может попасться задача о кредитах: например, на поиск суммы платежа, процентной ставки или срока. Также в этом номере вы можете встретить задачу на вклады или оптимизацию. Решение потребует большого количества вычислений, поэтому развивайте навык быстрого счёта.

Одно из самых сложных заданий ЕГЭ по профильной математике 2021 — №18. Это задача с параметром. В школе эту тему часто обходят стороной. Прежде чем приниматься за решение, нужно хорошо повторить функции, их свойства и графики.

Задание №19 — нестандартная задача, можно сказать, олимпиадного уровня. Она проверяет умение строить и исследовать простейшие математические модели. Вам помогут логика и хорошее знание математики в целом.

Советы по подготовке к ЕГЭ по профильной математике 2021

Повторите теорию

Не откладывайте на потом. Вспомните все определения, формулы и понятия перед там, как приступать к решению задач. Попробуйте писать формулы по памяти, а потом сверять

И не забывайте: важно не вызубрить темы, а понять их. 

Не пропускайте первую часть

Одна из грубых ошибок — переходить сразу к решению второй части ЕГЭ. Многие задачи из первой решаются довольно просто, но не стоит их недооценивать. Они составлены так, чтобы проверить не только навык решения, но и внимательность к деталям. Прорабатывайте номера из первой части, ведь для достижения цели важен каждый балл. 

Внимательно читайте текст заданий

Смотрите, в каких единицах измерения требуется ответ и нужно ли его округлять

В задании №7 важно понимать, какой график вам дан — производной или функции. От этого зависит ответ на заданный вопрос

В экономической задаче №17 нельзя использовать готовую формулу. Вам нужно написать математическую модель самостоятельно.

Научитесь хорошо считать в уме

Учитесь вычислять без калькулятора — некоторые задания требуют навыка быстрого счёта. К тому же, на экзамене вам нужно оставить как можно больше времени на сложные задачи и проверку.

Проверяйте решения и ответы

Например, убедитесь, что правильно перевели число из обычной дроби в десятичную. Арифметические ошибки также часто встречаются в задаче на финансовую математику

В задании №9 обратите внимание на знаки, особенно если вам попались тригонометрические функции

Также важно без ошибок определить ограничения x в задаче №13. Если исходное уравнение содержит tgx, то — cosx≠0

Если уравнение содержит квадратный корень, подкоренное выражение — ≥0

Если исходное уравнение содержит tgx, то — cosx≠0. Если уравнение содержит квадратный корень, подкоренное выражение — ≥0.

Проверяйте свои знания

Вы можете пройти тест на бесплатном вводном занятии с преподавателем или на сайте ФИПИ. Так вы узнаете, что помните хорошо, а что нужно повторить. Также вы можете воспользоваться нашей библиотекой знаний с полезными материалами для подготовки. Нужно только зарегистрироваться на сайте. 

Не бойтесь второй части 

Смело решайте задания из второй части. Попробуйте справиться с заданиями №13 и №15. Скорее всего, они вам хорошо знакомы. Чаще всего №13 оказывается не таким уж и сложным. Если вы хорошо знаете геометрию, начните с №14 или №16. Если вам по душе алгебра, решайте задачи на параметр и свойства чисел — №18, 19.

Отдыхайте 

Составьте комфортное расписание занятий. Подготовка к ЕГЭ по профильной математике в 2021 не должна быть тяжким бременем. Проводите больше времени на свежем воздухе, встречайтесь с друзьями и не забывайте про здоровый сон. 

I часть ЕГЭ по физике

Многие школьники готовятся только ко второй части экзамена. Думают, если вторую часть они могут решать, то и первая просто решится… Такие ученики ошибаются в простых заданиях, а для поступления в вуз мечты важен каждый балл! Ни в коем случае не стоит недооценивать первую часть.

Не стоит считать, что первая часть слишком простая и к ней можно не готовиться. Если пренебрежительно относиться к первой части, экзамен можно завалить, даже если вы решите всю вторую часть. Помните, что первая тестовая часть — это ⅔ всего экзамена.

В этой статье мы уже рассказывали, что можно набрать 80+ баллов, если сделать полностью первую часть, а вторую решить лишь на 40%.

В первой части есть задания базового уровня на 1 балл и повышенного уровня на 2 балла.

Задания базового уровня на 1 балл

Обычно такие задания решаются применением 1-2 физических законов и формул. Именно с заданий базового уровня я советую начинать. Как только вы прошли одну тему по физике, сразу же приступайте к решению задач формата ЕГЭ по этой теме!

Задания повышенного уровня на 2 балла

Первая часть ЕГЭ по физике включает в себя задания трех типов:

• Выбор 2 из 5 утверждений
• Анализ изменения величин
• Установление соответствия

Подробные разборы каждого типа заданий читайте в нашей предыдущей статье.

Стоит отметить, что в ЕГЭ можно все аргументировать, объяснить или опровергнуть. Как на дебатах. Только способ объяснения — это формулы и математические вычисления.

Электростатика и электродинамика – формулы по физике

Закон Кулона F=k∙q1∙q2/R 2 Напряженность электрического поля E=F/q Напряженность эл. поля точечного заряда E=k∙q/R 2 Поверхностная плотность зарядов σ = q/S Напряженность эл. поля бесконечной плоскости E=2πkσ Диэлектрическая проницаемость ε=E0/E Потенциальная энергия взаимод. зарядов W= k∙q1q2/R Потенциал φ=W/q Потенциал точечного заряда φ=k∙q/R Напряжение U=A/q Для однородного электрического поля U=E∙d Электроемкость C=q/U Электроемкость плоского конденсатора C=S∙ε∙ε0/d Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2 Сила тока I=q/t Сопротивление проводника R=ρ∙ℓ/S Закон Ома для участка цепи I=U/R Законы послед. соединения I1=I2=I, U1+U2=U, R1+R2=R Законы паралл. соед. U1=U2=U, I1+I2=I, 1/R1+1/R2=1/R Мощность электрического тока P=I∙U Закон Джоуля-Ленца Q=I 2 Rt Закон Ома для полной цепи I=ε/(R+r) Ток короткого замыкания (R=0) I=ε/r Вектор магнитной индукции B=Fmax/ℓ∙I Сила Ампера Fa=IBℓsin α Сила Лоренца Fл=Bqυsin α Магнитный поток Ф=BSсos α Ф=LI Закон электромагнитной индукции Ei=ΔФ/Δt ЭДС индукции в движ проводнике Ei=ВℓΥSinα ЭДС самоиндукции Esi=-L∙ΔI/Δt Энергия магнитного поля катушки Wм=LI 2 /2 Период колебаний кол. контура T=2π ∙√LC Индуктивное сопротивление XL=ωL=2πLν Емкостное сопротивление Xc=1/ωC Действующее значение силы тока Iд=Imax/√2, Действующее значение напряжения Uд=Umax/√2 Полное сопротивление Z=√(Xc-XL) 2 +R 2

Оптика

Закон преломления света n21=n2/n1= Υ1/ Υ2 Показатель преломления n21=sin α/sin γ Формула тонкой линзы 1/F=1/d + 1/f Оптическая сила линзы D=1/F max интерференции: Δd=kλ, min интерференции: Δd=(2k+1)λ/2 Диф. решетка d∙sin φ=k λ

Квантовая физика

Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=Uзе Красная граница фотоэффекта νк = Aвых/h Импульс фотона P=mc=h/ λ=Е/с

Физика атомного ядра

Закон радиоактивного распада N=N0∙2 — t / T Энергия связи атомных ядер

t=t1/√1-υ 2 /c 2 ℓ=ℓ0∙√1-υ 2 /c 2 υ2=(υ1+υ)/1+ υ1∙υ/c 2 Е = mС 2

Формулы по физике для егэ 2021 с пояснениями по заданиям

Вход в тесты

Более 2000 тестов с видео-решениями по математике. Более 1000 — по физике.

Подготовка к ЕГЭ. Подготовка к ОГЭ (бывший ГИА).

Справочник

Формулы, теоремы, решение типовых заданий…

На нашем WiKi-справочнике есть разделы по: геометрии, стереометрии, алгебре, физике и др.

Проверь себя

Проверьте себя самостоятельно!

Насколько хорошо Вы (или ваши дети) знают предмет?

А Вы готовы к контрольной?

Записаться на занятия

Телефоны:

• +7 (910) 874 73 73 +7 (905) 194 91 19 +7 (831) 247 47 55

• По математике
  • Подготовка к ЕГЭ Подготовка к ОГЭ Онлайн тесты к ЕГЭ и ОГЭ Формулы к ЕГЭ

По физике

• Подготовка к ЕГЭ Формулы для ЕГЭ Репетитор студенту

По скайпу

• Репетитор онлайн «Видео Репетитор»

Новости

• Новости образования Расписание ЕГЭ 2017 Расписание ОГЭ 2017 Расчёт баллов по ОГЭ 2015 Минимальные баллы 2015 Статьи 2012-2015
  • ГИА
    • Расписание ГИА 2013 Расписание ГИА 2014

ЕГЭ

• Расписание ЕГЭ 2015 Расписание ЕГЭ 2014 Расписание ЕГЭ 2013 ЕГЭ по физике

Обучение

• Аренда сайта Лекции онлайн Преподавателям

Стоимость О нас Контакты

За одного скидка 15%

За двоих скидка 30%!

«Ученье свет, а неученье — тьма»

Александр Васильевич Суворов

+7 (910) 874-73-73

X=X0+Υ0∙t+(a∙t 2 )/2 S= (Υ 2 —Υ0 2 ) /2а S= (Υ+Υ0) ∙t /2

Формулы по физике для ЕГЭ

Электроемкость C q U.

25.05.2017 18:03:22

2017-05-25 18:03:22

Тригонометрия

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Определение косинуса:

Определение тангенса:

Определение котангенса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:

Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Тригонометрические формулы сложения

Синус суммы:

Синус разности:

Косинус суммы:

Косинус разности:

Тангенс суммы:

Тангенс разности:

Котангенс суммы:

Котангенс разности:

Тригонометрические формулы преобразования суммы в произведение

Сумма синусов:

Разность синусов:

Сумма косинусов:

Разность косинусов:

Сумма тангенсов:

Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Произведение синусов:

Произведение синуса и косинуса:

Произведение косинусов:

Формулы понижения степени

Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

Формулы приведения задаются в виде таблицы:

Что в итоге

Теперь вы знаете больше про ЕГЭ по математике 2022

Вы познакомились со структурой и поняли, на что стоит обращать внимание при подготовке. А еще узнали, что первую часть обязательно решать на максимум, а вторая не такая страшная, как кажется

Но наверняка у вас еще осталась куча вопросов: по оформлению и конкретному решению каких-то заданий точно.Обо всем этом я подробно рассказываю своим ученикам во время подготовки к ЕГЭ по математике. Мы изучаем все непонятные темы, а потом прорешиваем много однотипных заданий — так легче запоминается формат. Еще мы всегда проводим пробные экзамены, чтобы выявить слабые места. Я анализирую ошибки каждого ученика и индивидуально разбираю их с ними. Благодаря этому мои выпускники гарантированно сдают ЕГЭ на 80+. Если вы хотите оказаться среди них — записывайтесь на курсы!