Степень изученности темы (разработанности проблемы) курсовой работы + пример

Предыстория

В конце декабря, к нам обратился «ВСоЗнании» — кемеровский некоммерческий фонд, который поддерживает и развивает городские сообщества. Они решили провести «Акселератор городских креативных событий». Это проект для руководителей кемеровских некоммерческих мероприятий, которые делают лучше жизнь горожан: любительских литературных и киноклубов, сообществ урбанистов, любителей истории, туризма, роботостроения.

В рамках проекта Фонд оценивает перспективы и социальную значимость проектов, обучает организаторов собирать аудиторию, предоставляет финансовую поддержку для реализации идеи самым целеустремленным.

Для старта проекта нужно было получить минимум 50 заявок от организаторов мероприятий Кемерова с понятным описанием их идеи. Причём участники должны быть готовы в течение нескольких месяцев посещать занятия Акселератора.

Фонд обратился к нам за помощью: нужно рассказать активным жителям Кемерово об Акселераторе и стимулировать их принять участие в проекте.

Шаг 3. Приводим к целевому действию

Следующий шаг — настроить ретаргетинг на тех, кто был на сайте, но пока не оставил заявку. Для этого ещё до старта установили пиксель ВКонтакте и настроили рекламу на собранную аудиторию.

На этом этапе уже не было необходимости тестировать гипотезы о поведении аудитории: все, кто зашёл на сайт, автоматически относятся к заинтересованной аудитории, ещё не готовой действовать.

Для перевода людей к активным действиям в объявлении сделали упор на срочность и ограниченность предложения.

Тестировали форматы объявлений:

• посты в ленте,
• тизеры,
• лид-формы.

Посты в ленте

Для ретаргетинга мы решили совместить рациональный подход в тексте и эмоциональный — в изображении к посту.

Ведь как мы выяснили на первой итерации, формат «пост в ленте» эффективен, если в нём есть юмор, а изображение не статично.

Для теста сформировали два варианта объявления с разными гиф-изображениями

В одном посте на изображении герой резко обращает внимание на пользователя, будто внезапно заметил. В другом посте персонаж анимации оглядывается по сторонам и скрывается.

По тестам первое объявление в показах и кликах проиграло второму. Персонаж, который скрывался с экрана, привлёк больше внимания.

Результат для поста с анимацией, где герой внезапно поворачивается на камеру.

Результат для поста с анимацией, где герой исчезает с экрана.

Как видим, и по кликабельности, и цене клика второе объявление превзошло первое в практически 4 раза. Стоимость клика была для нас допустимая, мы продолжили работу с этим форматом объявлений.

Важный момент: мы не были уверены, что для тёплой аудитории формат «пост в ленте» столь же эффективен, как и для холодной. Поэтому мы тестировали несколько объявлений с одинаковым подходом, но разными изображениями.

Если бы мы запустили для проверки только один пост, мы бы разочаровались в формате: 50 рублей за клик и всего 1 переход на сайт — слишком дорого. Параллельный запуск нескольких креативов позволил ориентироваться не на абстрактную приемлемую цену клика, а на реальные объявления и их статистику.

Тизеры

Тизеры в этом случае получили больше трафика, чем посты. Это очередное подтверждение, что тизеры отлично работают на аудиторию, которая знает о продукте и которую нужно подтолкнуть к нужному решению.

Сложность с тизерами в том, что прогрессирует баннерная слепота и объявления нужно умудриться сделать достаточно заметными среди всех прочих.

Первое, на что обращают взгляд в тизерах — изображение

По поверьям рекламщиков, люди в первую очередь обращают внимание на рекламу, где есть человек или животные, даже если видит их периферическим зрением. С другой стороны, этим подходом пользуются многие, а значит объявления с людьми и животными теряются среди других

Мы решили проверить, действительно ли это так и протестировали визуалы с животным, человеком и крупно написанным словом.

Примеры — *Пиксель 2, *Пиксель 3 и *Пиксель 4

Наибольший результат дало объявление с крупно написанным словом, что подтвердило нашу гипотезу: да, люди обращают внимание на людей и животных, но этот приём заезженный. Выделиться помогает объявление с нестандартным креативом.

Параллельно протестировали тизер, подчёркивающий ограниченность предложения. Это объявление показало максимальную эффективность среди всех тизеров ретаргетинговой кампании: было самым дешёвым по цене клика и получило наибольшее количество переходов.

*Пиксель 1

Лид-форма

Ещё одна гипотеза для ретаргетинга: пользователю неудобно заполнять форму на сайте. Решили упростить процесс регистрации и использовали лид-форму во ВКонтакте.

Этот формат не сработал: люди не оставляли заявки через лид-форму.

Особенности составления гипотезы в проектной работе

Рассмотрим особенности, которые существуют при подготовке гипотезы:

1. Гипотеза в проектной работе напрямую зависит от темы исследования, не может затрагивать не рассматриваемую в проекте информацию.
2. Гипотеза может касаться причин возникновения и существования объекта исследования, его свойств и связей, прошлого и будущего исследуемого объекта и т.д.
3. Гипотеза является научным предположением, которое выдвигается для предварительного, условного объяснения каких-либо фактов, событий, явлений и процессов, предполагающим доказательство либо опровержение.
4. Гипотеза может быть предположением, имеющим обоснование о том, как, каким путем, за счет чего можно получить искомый результат.
5. Предварительно выдвинутая гипотеза предопределяет логику всего процесса выполнения проектной работы, влияет на теоретическую и практическую часть работы.

Проверка гипотезы о воспроизводимости опытов

При проведении
экспериментов необходимо, чтобы опыты были воспроизводимы, т.е. результаты
опытов, поставленных в одинаковых условиях, не имели существенных различий.

Выбираем нулевую гипотезу
H: опыты воспроизводимы и альтернативную
гипотезуH₁ : опыты не воспроизводимы.

Для проверки справедливости
H ставится N-серий экспериментов, в каждой серии по m-параллельных опытов. Параллельными
называются опыты, проводимые в одинаковых условиях, т.е. при одних и тех же значениях
входных переменных. Следовательно, в факторном пространстве выбирается N точек и в каждой точке проводится по
m опытов. Результаты экспериментов
заносятся в таблицу:

Таблица 2.

№серии	Результаты экспериментов
1 2  N	Y11 Y12 … Y1m Y21 Y22 … Y2m YN1 YN2 … YNm

— оценка математического ожидания результатов
эксперимента в i-ой серии.

— оценка дисперсии результатов эксперимента в i-ой серии.

Для проверки нулевой
гипотезы выбирается критерий Кохрена (G):

.

По таблице распределения
критических точек критерия Кохрена в зависимости от уровня значимости q, числа степеней свободы f=m-1 и числа серий N определяем критическую точку:

G_kp= G (q, f, N).

По результатам
эксперимента вычисляем наблюдаемое значение критерия:

.

Если G_набл<G_кр, то гипотеза H принимается, в противном случае принимается
H₁. Если гипотеза H не принята, то для воспроизводимости
результатов эксперимента необходимо или повысить число параллельных опытов m, или увеличить точность измерения переменной
состояния. Если опыты воспроизводимы, то вычисляется ошибка опыта (дисперсия
воспроизводимости опытов)

.

Дисперсия
воспроизводимости опытов S2 является оценкой дисперсии переменной состояния s_y2.

Число степеней свободы
дисперсии воспроизводимости: f=N(m-1).

В некоторых лабораторных
экспериментах повторные измерения отклика в параллельных опытах дают один и тот
же результат . Тогда для расчета дисперсии воспроизводимости можно
воспользоваться метрологическими характеристиками измерительных приборов. В
паспортных данных прибора указывается класс его точности ( K , % от предела измерения ). Это позволяет определить
максимальную ошибку измерения

. (1)

Случайная ошибка прибора
подчиняется нормальному закону распределения . В машиностроении обычно
считается , что , при
этом вероятность попадания в интервал  равна 0,9973 и является технической единицей.

В
радиоэлектронной аппаратуре стабильность параметров активных и пассивных
элементов значительно ниже и надежность 0,95 вполне приемлема. Поэтому выбираем
. Подставляя значение в выражение (1), получим
дисперсию

.

Дисперсию
воспроизводимости полагаем равной

.

Пример:

Проверить гипотезу о
воспроизводимости опытов, в которых переменная состояния yзависит от трех факторовx₁ , x₂ , x₃. Выбрать уровень значимости q=0,05.

Проведены 8 серий по 2
параллельных опыта в каждой серии. Результаты эксперимента и расчеты сведены в таблицу:

Таблица 3.

№ серии	X1	X2	X3	Y1	Y2		Si2
1	0.40	0.20	24.00	0.71	0.77	0.74	0.001800
2	0.40	0.38	36.00	0.61	0.54	0.58	0.002450
3	0.40	0.38	24.00	0.65	0.59	0.62	0.001800
4	0.40	0.20	36.00	0.75	0.72	0.74	0.000450
5	0.60	0.20	24.00	0.73	0.64	0.69	0.004050
6	0.60	0.20	36.00	0.90	0.79	0.84	0.006050
7	0.60	0.38	24.00	0.74	0.71	0.73	0.000450
8	0.60	0.38	36.00	0.80	0.78	0.79	0.000200

Для каждой серии опытов
вычисляем среднее значение  и дисперсии результатов S_i2 . Далее выбираем  и вычисляем

 .Наблюдаемое значение критерия:

.

Значение критерия Кохрена
по таблице: G_кр=0.82.

Так как G_набл<G_{кр ,}то нулевая гипотеза Hпринимается.

Опыты воспроизводимы.
Ошибка опыта S2=0.0021562.

Проверка гипотезы о нормальном распределении ошибок эксперимента

Как правило, ошибки
результатов экспериментов распределены по нормальному закону .

Выберем следующие
гипотезы:

H: ошибки эксперимента распределены по
нормальному закону;

H₁: ошибки эксперимента не распределены
по нормальному закону.

Для проверки гипотезы H используется W–критерий.

Пусть проведено mпараллельных опытов ( 3 £m£ 50 ).

 Для обработки
результатов эксперимента нужно:

1) Расположить значения переменной
состояния в неубывающем порядке:

y₁ £y₂ £ …£y_m .

2) Вычислить: .

3) Вычислить: 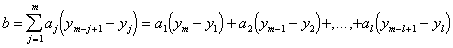где , если m-чётное и ,

если m-нечётное.

 Коэффициенты a_iвыбираются из таблицы в зависимости
от m.

4) Вычислить наблюдаемое значение критерия:

5) По таблице критических точек найти W_кр -критическое значение критерия в
зависимости от числа степеней свободы f= m и уровня значимости q:

W_кр= W(q, f );

6) Если наблюдаемое значение больше
критическогоW_набл >
W_кр (критическая область левосторонняя),
то гипотеза Hпринимается, т.е. ошибки эксперимента
распределены по нормальному закону. В противном случае, еслиW_набл<W_кр , то гипотеза Hотвергается.

Пример:

Проведено 16 параллельных
опытов. Получены следующие значения переменной состояния Y:

0.035 0.047 0.055
0.067 0.066 0.077 0.078 0.088

0.95
0.1 0.121
0.136 0.153 0.176 0.22 0.231

m = 16, q =
0,05, l = 16/2 = 8.

Отметим, что результаты
эксперимента расположены в неубывающем порядке.

;

;

где значения  для m = 16 взяты из таблицы: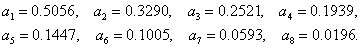

Наблюдаемое значение
критерия:

.

Критическое значение
критерия:

Так как W_набл>W_кр, , то ошибки эксперимента распределены
по нормальному закону.

Пример составления гипотезы в зависимости от класса или курса

Приведем примеры составления гипотезы для различных классов и курсов, для примера будет использоваться тема, которую могут рассматривать обучающиеся любого возраста.

Влияние пластика на природу.

Гипотеза для учащихся начальной школы (1-4 классы) может быть следующей:

Пример гипотез для 1-4 классов:

Мы предполагаем, что пластик оказывает влияние на природу.

Гипотеза для 5-6 классов должна быть более сложной, например:

Пример гипотез для 5-6 классов:

Мы предполагаем, что пластик оказывает негативное влияние не только на природу, но и человека.

Гипотеза для 7-8 классов должна более точно отражать изучаемый вопрос и показывать значимость темы проекта, например:

Пример гипотез для 7-8 классов:

Мы предполагаем, что пластиковые отходы оказывают негативное влияние на природу и организм человека, что связано с долгим периодом его разложения, поэтому на сегодняшний день так важно утилизировать пластиковые отходы. Гипотеза в проектных работах, выполненная учащимися 9-11 классов, должна включать в себя не только предположения, которое необходимо доказать или опровергнуть в ходе выполнения проекта, но и более детальное описание исследуемого вопроса с вероятным решением проблемы

Предполагаемое решение проблемы может быть не во всех гипотезах, что связано с отсутствием проблемы в исследуемой теме

Гипотеза в проектных работах, выполненная учащимися 9-11 классов, должна включать в себя не только предположения, которое необходимо доказать или опровергнуть в ходе выполнения проекта, но и более детальное описание исследуемого вопроса с вероятным решением проблемы. Предполагаемое решение проблемы может быть не во всех гипотезах, что связано с отсутствием проблемы в исследуемой теме.

Пример гипотез для 9-11 классов и колледжей:

Мы предполагаем, что пластиковые отходы в связи с большим сроком разложения наносят непоправимый вред всем живым организмам, засоряют Мировой океан, почву, оказывают отрицательное влияние на здоровье человека, поэтому в настоящее время важной является проблема переработки пластиковых отходов и уменьшения уже имеющихся захоронений пластика, что позволит очистить от него территории, которые в дальнейшем могут быть использованы человеком. Гипотеза в проектных работах для вузов должна быть более объемной и сложной, может содержать в себе несколько предположений, которые в ходе работы над проектом должны быть доказаны или опровергнуты, при этом основная гипотеза помещается в начало, далее следуют уточняющие или дополняющие основную гипотезу предположения

Каждая такая гипотеза имеет отдельную нумерацию и должна быть обособлена в абзаце

Гипотеза в проектных работах для вузов должна быть более объемной и сложной, может содержать в себе несколько предположений, которые в ходе работы над проектом должны быть доказаны или опровергнуты, при этом основная гипотеза помещается в начало, далее следуют уточняющие или дополняющие основную гипотезу предположения. Каждая такая гипотеза имеет отдельную нумерацию и должна быть обособлена в абзаце.

Что должно быть в основной части дипломной работы

Так как основная часть выпускной квалификационной работы представляет собой повествование о вашем исследовательском труде, то в ней необходимо отразить следующие сведения:

1. Выбор направления исследований, или проще говоря, какова тематика работы.
2. Обоснование своего выбора. То есть, почему вы решили выбрать именно эту тему и алгоритм работы.
3. Последовательное описание выполнения поставленных перед исследователем задач и результаты каждого этапа. В заключении нужно будет отразить их в скомпилированном виде.
4. Теоретические выкладки. В первую очередь, это гипотеза и описание того, что сподвигло вас на ее выдвижение.
5. Обоснование гипотезы — почему вы думаете, что она может быть верна, и как вы планируете это доказать.
6. Описание общей методики исследовательской работы. То есть, что вы делали для достижения тех или иных результатов, и каким образом.
7. Обоснование методики и технологий экспериментирования. Проще говоря, почему вы проводите исследование именно выбранными способами, а не какими-то другими.
8. Принципы действия того, что вы исследовали. То есть, почему ваше решение работоспособно и какие законы заставляют его действовать. Какие характеристики присущи результату вашей работы.
9. Оценочные суждения. В этой части описываются варианты применения вашего решения в исследуемой отрасли. Ваша оценка актуальности, нужности и полезности своей разработки должна быть обоснована «от и до», в том числе и экспериментальной частью.
10. Обоснование необходимости дальнейших исследований (если того требует отрасль и конкретно ваша работа). Это не обязательный момент, так как темой дипломной работы может быть и конечный продукт — например, фильм. Вряд ли есть смысл передавать эстафету следующим курсам, превращая дипломную короткометражку в многосерийное произведение.
11. Сравнение с аналогичными исследованиями в отрасли в России и за рубежом. Вы наверняка уже затрагивали этот момент во «Введении», но там он состоит из нескольких обобщенных фраз. В основной части сравнения помогают подтвердить, опровергнуть или уточнить конкретные тезисы и эксперименты.
12. Смело рассказываем о том, что не получилось. Например, при каких условиях монгольские песчанки отказались употреблять специально разработанный будущим ветеринаром корм. Или почему ваш уникальный реактив не среагировал на другое экспериментальное вещество. Несоответствие результата гипотезе — это не проигрыш, а вполне возможный прорыв в отрасли или ответ на вопрос, над которым долгие годы бьются лучшие умы. Поэтому не стесняйтесь писать о просчетах, они порой важны не меньше, чем успешные решения.
13. Если в «Заключении» выводы описываются тезисно, то в основной части работы их обязательно нужно развернуть. Что получилось в процессе решения той или иной задачи, как так вышло и что теперь с этим делать? Ответ на эти три вопроса должен быть дан либо в отдельном параграфе, либо по ходу закрытия этапов исследования.

(таблица критических точек критерия Фишера)

(F – распределение для уровня значимости q=0.05)

f2	f1
1	2	3	4	5	8	12	24	¥
1 2 3 4 5 6 7 8 10 12 16 20 60 ¥	164 18.5 10.1 7.71 6.61 5.99 5.50 5.32 4.96 4.75 4.49 4.35 4.00 3.84	199 19.0 9.55 6.94 5.79 5.14 4.74 4.46 4.10 3.88 3.63 3.49 3.15 2.99	215 19.2 9.28 6.59 5.41 4.76 4.35 4.07 3.71 3.49 3.24 3.10 2.76 2.60	224 19.2 9.12 6.39 5.19 4.53 4.12 3.84 3.48 3.26 3.01 2.87 2.52 2.37	234 19.3 8.94 6.16 4.95 4.28 3.87 3.58 3.22 3.00 2.74 2.60 2.25 2.09	239 19.4 8.84 6.04 4.82 4.15 3.73 3.44 3.07 2.85 2.59 2.45 2.10 1.94	243 19.4 8.74 5.91 4.68 4.00 3.57 3.28 2.91 3.69 2.42 2.28 1.92 1.75	249 19.4 8.64 5.77 4.53 3.84 3.41 3.12 2.74 2.50 2.24 2.08 1.70 1.52	254 19.5 8.53 5.63 4.36 3.67 3.23 2.93 2.54 2.30 2.01 1.84 1.39 1.00

Примечание. f₁ – число степеней свободы большей дисперсии, f₂ – число степеней свободы меньшей дисперсии.

Статистическая гипотеза. Статистический критерий. Ошибки, возникающие при проверке гипотез

Статистической называют гипотезу о виде
неизвестного распределения или о параметрах известного распределения.

Например, гипотеза H — случайная величина распределена по
нормальному закону.

Нулевой (основной) называется выдвинутая
гипотеза H.

Альтернативной (конкурирующей) называется гипотеза,
противоречащая основной (конкурирующих гипотез может быть несколько).

Например, основная
гипотеза — математическое ожидание случайной величины Y равно 5

HM_y=5,

конкурирующие:

H₁

H₂

H₃

Статистическим критерием
(К) называется случайная величина, точное или приближённое распределение,
которой известно и которая служит для проверки справедливости нулевой гипотезы.

Множество возможных
значений критерия делится на две непересекающихся области:

1) значения, при которых
нулевая гипотеза справедлива (область принятия гипотезы).

2) значения, при которых
нулевая гипотеза отвергается (критическая область).

Критическая область может
быть односторонней (левосторонней, правосторонней) или двусторонней.

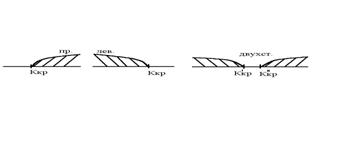
Рис.1. Виды критических
областей: правосторонняя, левосторонняя и двусторонняя.

Точка К_кр,
отделяющая критическую область от области принятия гипотезы, называется
критической точкой.

Чтобы определить
критическую область, выбирают число q-уровень значимости. q— вероятность того, что при справедливости нулевой
гипотезы значение критерия К попадает в критическую область. Тогда для
правосторонней критической области К_кр определяется из условия:

P { K > K_kp} = q.

Значение критерия
табулировано, т. е. K_kp можно найти по таблице распределения критических точек в
зависимости от уровня значимости q и числа степеней свободы f. -Наблюдаемое
значение критерия K_набл определяется
по результатам эксперимента.

Если K_набл<K_kp, то гипотеза Hпринимается. Если K_набл>K_kp, то H отвергается, а принимается конкурирующая
гинотеза H₁.

Для левосторонней
критической области критическая точка определяется из условия:

P { K < K_kp} = q.

Для двухсторонней:

P { K < K’_kp} + P { K > K”_kp} = q.

Если двусторонняя область
симметрична относительно начала координат, то:

P { K < K’_kp} = .

Так как наблюдаемое
значение критерия определялось по результатам эксперимента, то К_набл-случайная
величина и, следовательно, могут возникать ошибки при принятии гипотезы.
Различают ошибки первого и второго рода. К ошибкам первого рода относят те, при
которых отвергается правильная гипотеза. К ошибкам второго рода, относят те,
при которых принимается неправильная гипотеза. Допустимой вероятностью ошибки
первого рода является q-уровень
значимости. Однако. если уменьшать q, то возрастает вероятность принятия неверной гипотезы, т. е. вероятность
ошибок второго рода. Если справедлива гипотеза H₁, то это считается доказанным, если
справедлива гипотеза H-то
говорят, что результаты эксперимента не противоречат нулевой гипотезы. Для того
чтобы считать H доказанной нужно или вновь повторить
эксперимент или проверить гипотезу с помощью других критериев.

2. Порядок проверки
статистических гипотез

1) Выбор нулевой и
альтернативной гипотез H и H₁.

2) Выбор критерия K и уровня значимостиq.

3) Вычисление K_набл по результатам эксперимента.

4) ПоискK_kp по таблице распределения критических
точек для выбранного критерия.

5) Если K_набл попадает в критическую область, то
принимается альтернативная гипотеза H₁, если K_набл попадает в область принятия
гипотезы, то принимается основная гипотеза H.

(таблица значений функции Лапласа Ф(х))

(Таблица значений функции
 

x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)
0.00	0.0000	0.22	0.0871	0.44	0.1700	0.66	0.2454
0.01	0.0040	0.23	0.0910	0.45	0.1736	0.67	0.2486
0.02	0.0080	0.24	0.0948	0.46	0.1772	0.68	0.2517
0.03	0.0120	0.25	0.0987	0.47	0.1808	0.69	0.2549
0.04	0.0160	0.26	0.1026	0.48	0.1844	0.70	0.2580
0.05	0.0199	0.27	0.1064	0.49	0.1879	0.71	0.2611
0.06	0.0239	0.28	0.1103	0.50	0.1915	0.72	0.2642
0.07	0.0279	0.29	0.1141	0.51	0.1950	0.73	0.2673
0.08	0.0319	0.30	0.1179	0.52	0.1985	0.74	0.2703
0.09	0.0359	0.31	0.1217	0.53	0.2019	0.75	0.2734
0.10	0.0398	0.32	0.1255	0.54	0.2054	0.76	0.2764
0.11	0.0438	0.33	0.1293	0.55	0.2088	0.77	0.2794
0.12	0.0478	0.34	0.1331	0.56	0.2123	0.78	0.2823
0.13	0.0517	0.35	0.1368	0.57	0.2157	0.79	0.2852
0.14	0.0557	0.36	0.1406	0.58	0.2190	0.80	0.2881
0.15	0.0596	0.37	0.1443	0.59	0.2224	0.81	0.2910
0.16	0.0636	0.38	0.1480	0.60	0.2257	0.82	0.2939
0.17	0.0675	0.39	0.1517	0.61	0.2291	0.83	0.2967
0.18	0.0714	0.40	0.1554	0.62	0.2324	0.84	0.2995
0.19	0.0753	0.41	0.1591	0.63	0.2357	0.85	0.3023
0.20	0.0793	0.42	0.1628	0.64	0.2389	0.86	0.3051

0.88	0.3106	1.14	0.3729	1.40	0.4192	1.66	0.4515
0.89	0.3133	1.15	0.3749	1.41	0.4207	1.67	0.4525
0.90	0.3159	1.16	0.3770	1.42	0.4222	1.68	0.4535
0.91	0.3186	1.17	0.3790	1.43	0.4236	1.69	0.4545
0.92	0.3212	1.18	0.3810	1.44	0.4251	1.70	0.4554
0.93	0.3238	1.19	0.3830	1.45	0.4265	1.71	0.4564
0.94	0.3264	1.20	0.3849	1.46	0.4279	1.72	0.4573
0.95	0.3289	1.21	0.3869	1.47	0.4292	1.73	0.4582
0.96	0.3315	0.3883	1.48	0.4306	1.74	0.4591
0.97	0.3340	1.23	0.3907	1.49	0.4319	1.75	0.4599
0.98	0.3365	1.24	0.3925	1.50	0.4332	1.76	0.4608
0.99	0.3389	1.25	0.3944	1.51	0.4345	1.77	0.4616
1.00	0.3413	1.26	0.3962	1.52	0.4357	1.78	0.4625
1.01	0.3438	1.27	0.3980	1.53	0.4370	1.79	0.4633
1.02	0.3461	1.28	0.3997	1.54	0.4382	1.80	0.4641
1.03	0.3485	1.29	0.4015	1.55	0.4394	1.81	0.4649
1.04	0.3508	1.30	0.4032	1.56	0.4406	1.82	0.4656
1.05	0.3531	1.31	0.4049	1.57	0.4418	1.83	0.4664
1.06	0.3554	1.32	0.4066	1.58	0.4429	1.84	0.4671
1.07	0.3577	1.33	0.4082	1.59	0.4441	1.85	0.4678
1.08	0.3599	1.34	0.4099	1.60	0.4452	1.86	0.4686
1.09	0.3621	1.35	0.4115	1.61	0.4463	1.87	0.4693
1.10	0.3643	1.36	0.4131	1.62	0.4474	1.88	0.4699
1.11	0.3665	1.37	0.4147	1.63	0.4484	1.89	0.4706
1.12	0.3686	1.38	0.4162	1.64	0.4495	1.90	0.4713
1.13	0.3708	1.39	0.4177	1.65	0.4505	1.91	0.4719

x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)
1.92	0.4726	2.18	0.4854	2.52	0.4941	2.84	0.4977
1.93	0.4732	2.20	0.4861	2.54	0.4945	2.86	0.4979
1.94	0.4738	2.22	0.4868	2.56	0.4948	2.88	0.4980
1.95	0.4744	2.24	0.4875	2.58	0.4951	2.90	0.4981
1.96	0.4750	2.26	0.4881	2.60	0.4953	2.92	0.4982
1.97	0.4756	2.28	0.4887	2.62	0.4956	2.94	0.4984
1.98	0.4761	2.30	0.4893	2.64	0.4959	2.96	0.4985
1.99	0.4767	2.32	0.4898	2.66	0.4961	2.98	0.4986
2.00	0.4772	2.34	0.4904	2.68	0.4963	3.00	0.49865
2.02	0.4783	2.36	0.4909	2.70	0.4965	3.20	0.49931
2.04	0.4793	2.38	0.4913	2.72	0.4967	3.40	0.49966
2.06	0.4803	2.40	0.4918	2.74	0.4969	3.60	0.499841
2.08	0.4812	2.42	0.4922	2.76	0.4971	3.80	0.499928
2.10	0.4821	2.44	0.4927	2.78	0.4973	4.00	0.499968
2.12	0.4830	2.46	0.4931	2.80	0.4974	4.50	0.499997
2.14	0.4838	2.48	0.4934	2.82	0.4976	5.00	0.499997
2.16	0.4846	2.50	0.4938

1.Статистическая гипотеза. Статистический критерий. Ошибки, возникающие при проверке гипотез

2. Порядок проверки статистических гипотез

3. Проверка однородности результатов эксперимента в целях
исключения грубых ошибок

4. Проверка гипотезы о воспроизводимости опытов

5. Проверка гипотезы о нормальном распределении ошибок эксперимента

6. Проверка гипотезы о виде распределения. ( Критерий
согласия Пирсона )

6.1 Расчёт теоретических частот для нормального распределения

7.Проверка гипотезы о согласованности мнений экспертов
(априорное ранжирование переменных)

8. Уравнение линейной регрессии. Коэффициент корреляции.
Проверка гипотезы о значимости коэффициента корреляции

8.3 Использование корреляционной таблицы для вычисления
коэффициента корреляции

Вывод

Как правильно составить гипотезу в проектной работе

В связи с тем, что гипотеза – это предположение, которое должно быть либо подтверждено, либо опровергнуто необходимо правильно структурировать её, в том числе, важно правильно начать формулировку. Для правильной формулировки гипотезы можно использовать следующие вспомогательные словесные конструкции и слова:

Для правильной формулировки гипотезы можно использовать следующие вспомогательные словесные конструкции и слова:

• В связи с чем
• Возможно
• Допустим
• Если …, то …
• Можно предположить
• Мы предполагаем
• По этой причине
• Поэтому
• Предположим
• При условии, что…
• Так как…
• Чем…, тем…
• Что, если

Пример использования приведённых слов и словесных представлен ниже.

Использование слов и совесных конструкций в гипотезе проектной работы

Использование предложенных слов и словесных конструкций не является обязательным, но может помочь правильно сформулировать гипотезу, ведь её правильная формулировка облегчит выполнение проектной работы, при этом неправильно сформулированная гипотеза приведет к ложному результату, может потребовать частичной или полной переработки проектной работы.

Как быстро написать основную часть дипломной работы

Исследование проведено, накопилась гора материала, которую нужно красиво и последовательно описать в своем отчете по НИР. Как это сделать быстро? Нужно просто действовать по плану.

Шаг 1

Составляем черновик. В первую очередь, делим всю работу условно на три части:

1. Теоретические выкладки. Гипотеза, рассуждения и предположения — все собираем в этом разделе. Сравнение своих идей с трудами других ученых — сюда же, как и планирование.
2. Практическая часть. Последовательное проведение эксперимента, расчеты, выкладки, методики и их изменения в ходе работы (а также обоснование данных изменений) — все это отправляется в данный раздел.
3. Выводы и рекомендации. Развернутое представление результатов практической части и рассуждения о том, что можно было бы поменять. Сравнение с результатами других экспериментов отправляем в этот раздел.

Теперь распределяем по ним весь имеющийся массив данных. Получилось три больших раздела с информацией по вашему отчету. Их можно выделить прямо так, как указано в нашем списке.

Если специфика работы не предполагает распределения на три раздела, то можно оставить описанное выше разделение как условное для каждого структурного элемента основной части отчета. В этом случае нужно поделить практику исследования на главы, обозначающие последовательность действий, либо описывающие выполнение определенных задач. В этом случае делаем внутри глав условное деление на теорию/практику/результат.

Шаг 2

Для каждого раздела составляем последовательность написания данных.

1. Для теоретических выкладок. Начинаем с гипотезы, обосновываем ее, сравниваем и т.д. План работ описываем перед практической частью, чтобы обеспечить логическую последовательность повествования.
2. Для практики. Описываем проведение эксперимента/исследования с первых шагов и до анализа полученных данных. По каждой задаче делаем отдельный параграф/подглаву. Общую аналитику пишем перед разделом с результатами, чтобы все выглядело логично — задача, выполнение, анализ, вывод.
3. Для выводов. Компиллируем результаты и составляем рекомендации. Общее резюме и итоги отдельных задач пишем в той последовательности, которую считает нужной ваш ВУЗ, либо вы сами (если указаний на эту тему нет).

Если мы не делили основную часть на три раздела, а вводили их в структурные элементы, то описанная схема переносится внутрь параграфов и подглав.

Шаг 3

Теперь поработаем над наглядными материалами. Нам предстоит решить, что оставить в тексте дипломной работы, а что отправить за пределы основной части — в структурный элемент «Приложения». Если вы не знаете, как лучше это сделать — почитайте нашу статью по этой теме. Рекомендуем проводить эту работу непосредственно с научным руководителем.

Шаг 4

Сверяемся со списком литературы, списком терминов, сокращений и обозначений, и учебником русского языка. Выковыривать потом из чистового варианта неправильно проставленные запятые — удовольствие сомнительное, так что занимаемся этим на стадии черновика. На этом шаге вы сможете отработать комбинацию клавиш «ctl+C -> ctl+F -> ctl+V» до уровня рефлекса.

Шаг 5

Предчистовая подготовка. Теперь, когда черновой вариант готов и уже похож на последовательное повествование с намеченной структурой, можно заняться красотой текста. Проходимся от начала до конца и правим неловкие выражения, лишние сокращения. Добавляем пояснения и подписи к наглядным материалам внутри текста, нумеруем структурные элементы. На этом этапе рекомендуется составить начальный вариант содержания без простановки номеров страниц.

Этот пример выпускной квалификационной работы уже можно нести на одобрение к научному руководителю.

Пример.docx (cкачиваний: 115)

Шаг 6

Делаем чистовик. Вносим указанные научным руководителем правки, исправляем последние попавшиеся на глаза ошибки. Основная часть диплома готова. Настало время для написания других структурных элементов.

Чтобы узнать, как правильно оформить курсовую, дипломную или выпускную квалификационную работу — читайте нашу общую статью по этой теме. В ней вы узнаете много нового и сможете подробнее ознакомиться с публикациями про другие структурные элементы НИР.

Проверка гипотезы о виде распределения. ( Критерий согласия Пирсона )

Пусть проведены N экспериментов в одинаковых условиях.
Проверяется гипотеза H результаты эксперимента распределены
по закону А. Критерий для проверки выдвинутой гипотезы называется
критерием согласия.

Разобьем интервал
полученных результатов эксперимента Y_min, Y_max на m равных
интервалов.

Y_{i -1} , Y_i]; i=1,…,m.

Обозначим через Y_i* середину i-го интервала, n_i— число результатов, попавших в i-й интервал. Получим ряд
распределения:

Yi*	Y1*	Y2*	…	Ym*
ni	n1	n2	…	nm

Пусть в предположении,
что результаты эксперимента имеют распределение А, вычислены теоретические
частоты n_i’.

В качестве статистического
критерия выбирается случайная величина:

Чем меньше значение,
принимаемое c2, тем ближе между собой теоретическое и эмпирическое распределения.
Случайная величина c2 имеет известное распределение Пирсона или c2_.— распределение.

Критическое значение
критерия определяется по таблице распределения критических точек по заданному
уровню значимости q
и числу степеней свободы f:

f = m—r-1;

где r-число параметров распределения,
определяемых по результатам эксперимента. Для нормального распределения r=2, для распределения Пуассона и показательного
распределения r=1.

Наблюдаемое значение
критерия c2_набл рассчитывается по результатам
экспериментов

.

Если c2_набл<c2_кр, то гипотеза Hпринимается, т. е. результаты эксперимента
распределены закону А . Если c2_набл>c2_кр, то H-отвергается (критическая область
правосторонняя).

6.1
Расчёт теоретических частот для нормального распределения

1. Вычисляем оценки
математического ожидания и дисперсии:

2. Вычисляем границы
интервалов нормированной переменной Z:

, i = 0,1,…., m.

3.   Выберем по таблице значения функции
Лапласа Ф(Z_i);

4.   Найдём вероятность попадания значений
нормально распределённой случайной величины Z в i-й
частичный интервал:

5.   Вычисляем теоретические частоты: .

Пример:

Пусть даны результаты 75
экспериментов. Проверить гипотезу о нормальном распределении результатов
экспериментов:

-50	-39	-48	-56	-49
-44	-39	-42	-56	-46
-39	-50	-52	-48	-55
-46	-37	-51	-52	-45
-46	-51	-43	-49	-35
-57	-48	-42	-54
-33	-44	-56	-44	-43
-41	-47	-42	-47	-59
-54	-53	-55	-34	-53
-50	-36	-53	-53	-55
-54	-39	-53	-42	-49
-45	-48	-50	-48	-56
-52	-46	-53	-56	-57
-42	-53	-50	-44	-46
-59	-62	-57	-36	-43

	Начало первого интервала:	-64
	Длина интервала:	4

Разобьем интервал
на частичные интервалы с шагом, равным 4. Для каждого частичного интервала
подсчитаем число результатов, попавших в данный интервал. Обозначим эти частоты
n_i. Вычислим середины частичных интервалов
.

Полученные
результаты вычислений занесем в таблицу.

Находим
оценки математического ожидания и среднего квадратического отклонения (1/75)·(-65-290-972-650-644-788-190-170)
=

= -3566/75=-47.54;

где Y*_i – середина i -го интервала.

(1/74)×(209.09+547.058+751.1688+

+78.6708+33.2024+429.6824+455.058+916.658)
= =3420.5884/74=46.224 ;

S_y = 6.7988=6.80;

Вычислим границы
интервала в кодированных переменных:

.

Вероятность попадания
нормально распределённой случайной величины в i-тый частичный интервал

P_i= Ф(Z_i+1) — Ф(Z_i); i=1,…,m,

где Ф(z) — функция Лапласа.

Вычислим теоретические
частоты n_i‘ =N×P_i.

Величины Z_i, P_i
и n_i‘
заносим в таблицу.

Определим наблюдаемое
значение критерия

K_набл= 0,9168
+ 0,0526 + 4,008 + 0,69 + 0,4303 + 0,1555 + 0,3874 + 0,74137) = 7,38197;

Найдём критическое
значение критерия Пирсона для уровня значимости q=0.1 и числа степеней свободы

f=m-2-1=8-2-1=5:

K_кр=c2 (q,f)= c2(0.1;5)=9.236.

Таблица 4.

№		ni		Z i	Ф(Z i)	Pi	ni1	ni	(ni1-ni)2  ni1
1 2 3 4 5 6 7 8	-64 -60 -56 -52 -48 -44 -40 -36 -32	1 5 18 13 14 14 5 5	-62 -58 -54 -50 -46 -42 -38 -34	-¥ -1.83 -1.24 -0.65 -0.06 0.52 1.11 1.69 +¥	-0.5 -0.4664 -0.3925 -0.2415 -0.0239 0.19847 0.3665 0.45449 0.5	0.0336 0.0739 0.1504 0.2182 0.2224 0.1680 0.0880 0.0455 åPi=1	2.52 5.54 11.277 16.36 16.679 12.6 6.599 3.41	1 5 18 13 14 14 5 5	0.9168 0.0526 4.008 0.69 0.4303 0.1555 0.3874 0.74137

Так как K_набл <
K_кр , то гипотеза H справедлива, т.е. результаты
эксперимента распределены по нормальному закону.